“Why there is continuity”

Introduction to the general theorem of continuity

6/8/14 draft –   Perhaps it just seemed too obvious to ask before, or maybe other scientists hadn’t found a reasonable way to do it.      Continuity underlies every principle of physics and all our observations of nature, that “things are connected” but also some how all “individual” and “disconnected” too.  Still, we find seemingly without exception that the future is built on the past and that change generally incorporates flowing processes of change, but working with all sorts of disconnected parts .    I found it particularly fascinating, that “flows” both contained and often turned out to become “disconnected parts” of larger scale flows, exposing how continuities and discontinuities appear to be mingled at every scale of natural designs.   My professors and equations simply never spoke about that.    The implications led me to:

• see continuity as a ladder of steps of change
• learning to examine finer and finer scales of connections
• exposing a number of new fields of interest where I could do original research
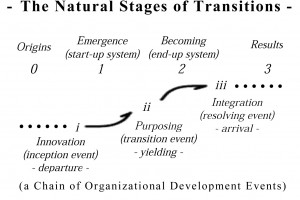
  • starting with closely examining “flows”
  • and their stages from beginning to end

the theorem

 A law of emergence and continuity in change

The way I eventually chose to answer “Why is there continuity?” was with a mathematical proof supported with readily available evidence.   The proof demonstrates that the “first principle of physics”, the  “conservation of energy”, implies that any individual event of finite duration needs to originate with a punctuated developmental burst of organization and energy flow.   Then the review of the evidence strongly suggests that so many of the observable kinds and scales of events clearly fit that model.   It suggests that events of all kinds must be predominantly be “individual” and “finite”, and so even when “predictable”, not “predetermined”.    The proof starts with:

• stating the conservation of energy as an equation of change over time,
• and then taking successive derivatives.

That produce

• an infinite chain of conservation laws
• including the other two commonly used ones,
  • the conservation of momentum and
  • the conservation of reaction forces.

The unexpected and all important discovery is that the simple statement of energy conservation, that the sum of energies within a system is constant and finite, implies that the rates of change of energy entering or leaving a system are finite if unconstant, and that,

• when reintegrating that infinite series of implications
  • for how change in any system is bounded
• the accumulation of integration constants produce a form of polynomial expansion
• defining a very general form of exponential or logarithmic curves for flowing transitions.

An important added ‘lemma’ can be left to the reader, that while change in nature is often usefully “predicted” by equations, the principle of continuity indicates that nature clearly cannot be “occurring” by equations.   What seems evident is nature operates by a process of making and then breaking her rules, not by following them as we need to use them for.

 

The principal evidence

The principal evidence is the everpresent “S curves” in our measurements of change, that when looked at closely reveal complex organization and with graduated accumulations of change.   The trick for following them is perhaps mostly to be patient in searching all the possibilities, as frequently what appear to be breaks in continuity are places where the connections are at some other scale, seen from some other view, or of some other kind.   Observation is ‘fragmentary’, but nature is ‘holistic’ in profound ways, and the question is then “Why?”

How one uses “the principle of continuity in change” I found is for

• generating focused questions about the ascending and then descending scale events
• and the corresponding swelling and then subsiding development of accumulative processes,
• that nature needs to accomplish any kind of physical change,

that serve to highlight in the data exactly where there has to be

• points of origination,
• diverging developmental processes,
• and converging developmental processes

 ______

p.s. 7/11/14

Links to more general Introductions & Guides:

Related posts introducing the natural cycle of system transformations and how to use them for researching and responding to the systems of our world include the most detailed general diagram: “Chapters of a whole event” and articles in the general category: “Scientific Theory“.   There’s also my “1990’s Archive of empirical studies” and the following recent more general introductions from various approaches:

1. In two words… what defines “science”?
2. Finding Organization in Natural Systems – “Quick Start”
3. 3Step process for Working With Nature
4. Tricky Reading – the Indicator & the Context
5. Missing Principles of Ecological Thinking – in plans for the Earth
6. Sustainability = growing profit then steady profit
7. Fresh Thinking for The Tragedy of the Commons
8. Multi-Stakeholder Partnerships
9. Steering for the organizational Lagrange Point
10. Steps to a natural systems view
11. Self-organization as “niche making”

JLH