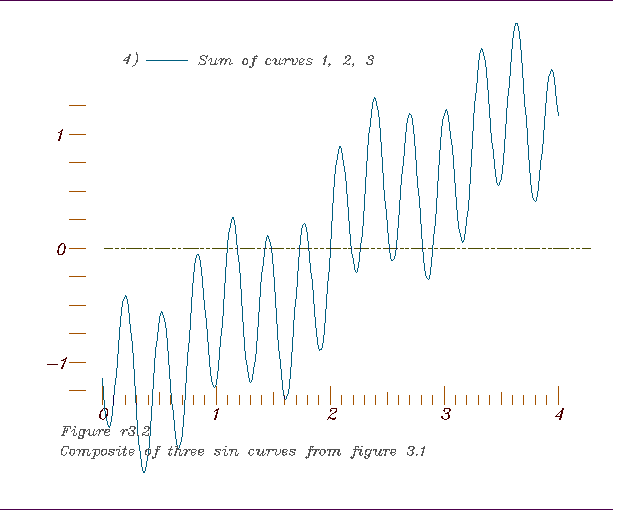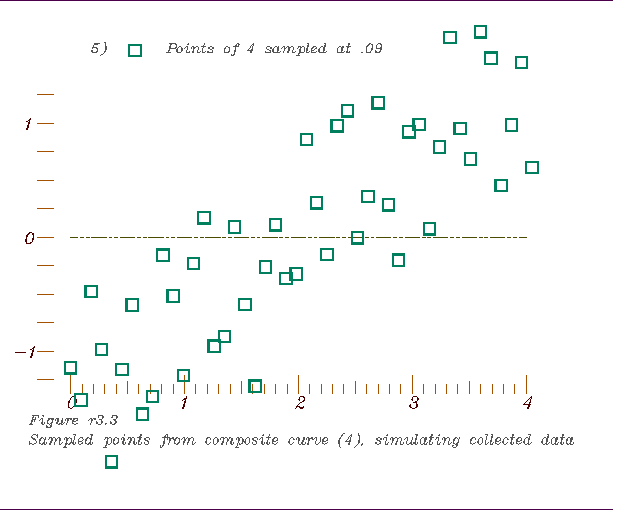Reconstructing a sampled composite function (full
size)
back
To test the DR method a sin curve is 'disguised' by superimposing two
other sin curves of higher frequency and then sampling values from the
composite to see if the components can then be reconstructed.
Normal curve fitting methods would treat the data produced this way
as statistically distributed around a single function, probably producing
a straight line and a random variable. A keen observer would note the cyclic
pattern in the data and might separate these very regular components. DR
works just as well when the data is real, with irregular, asymmetric and
transient underlying processes to be separated out.
The figures display the compound sin curve test procedure in12 steps:
(open two browsers to view figures side-by-side)
1. Selecting three regular mathematical functions,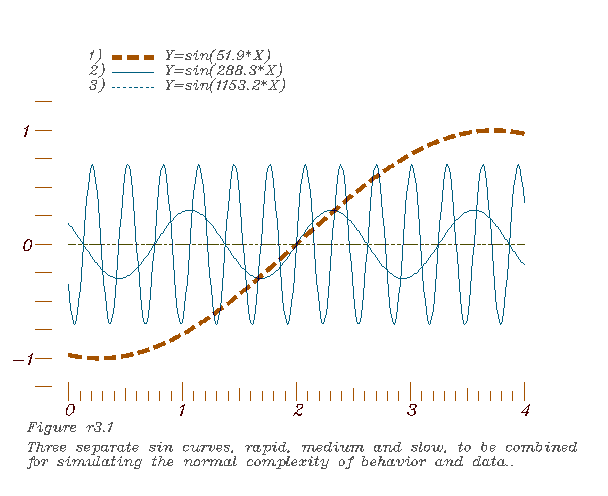
2. The composite to be sampled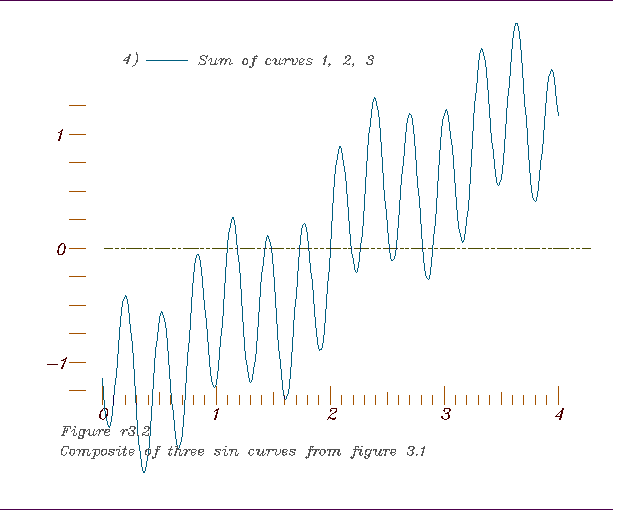
-
3. A periodic sampling of points to simulate a data set representing a
complex of processes.
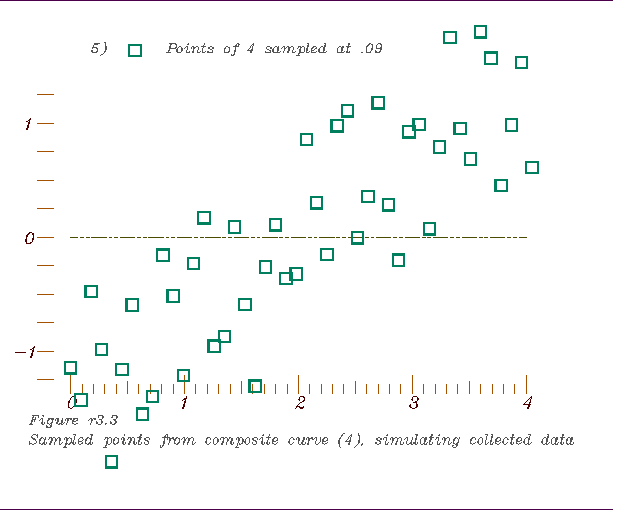 4. A graph of the selected points,
4. A graph of the selected points,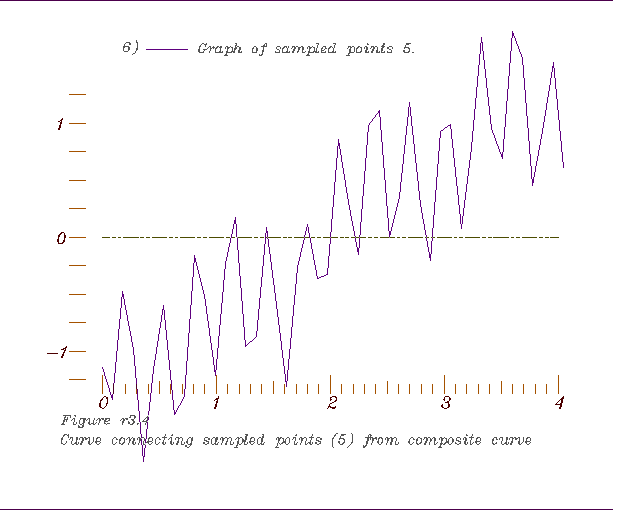 5. Derivative interpolation of the data and location of its inflection
points,
5. Derivative interpolation of the data and location of its inflection
points,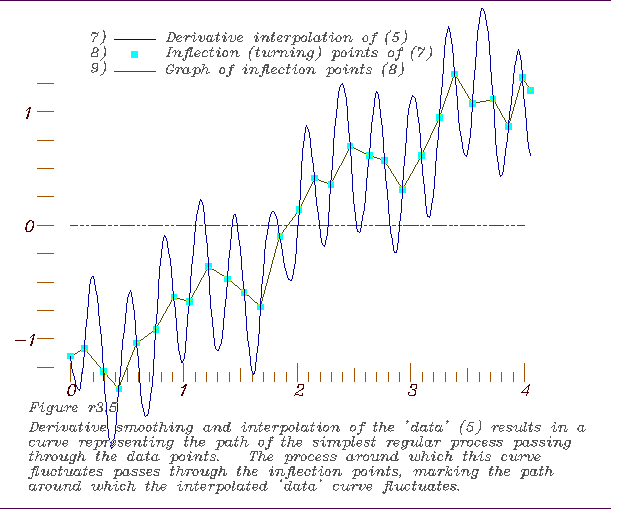 6. Derivative interpolation of those inflection points to form the 1st
dynamic mean,
6. Derivative interpolation of those inflection points to form the 1st
dynamic mean,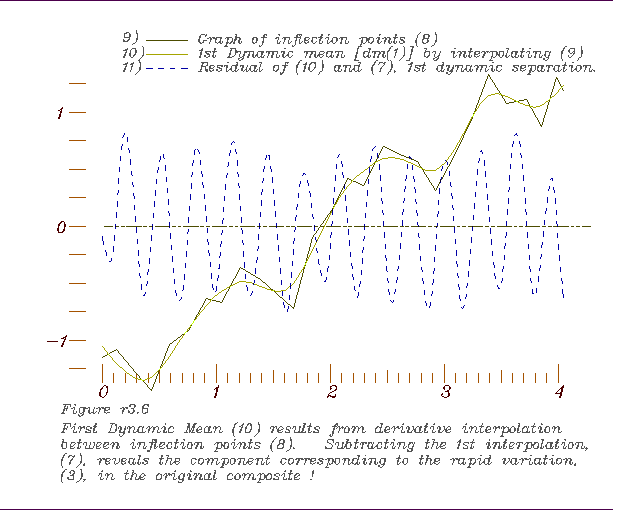 7. Inflection points of the 1st dynamic mean,
7. Inflection points of the 1st dynamic mean, 8. Derivative interpolation based on inflection points of 1st dynamic mean
to form the 2nd,
8. Derivative interpolation based on inflection points of 1st dynamic mean
to form the 2nd,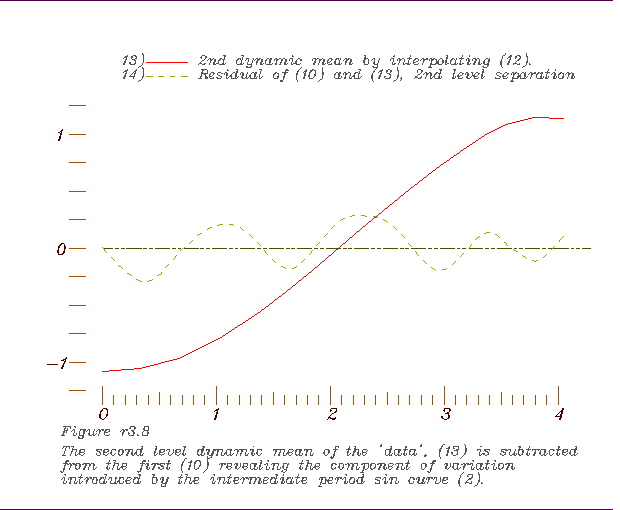 9. Comparing the 2nd dynamic mean with the long period sine curve.
9. Comparing the 2nd dynamic mean with the long period sine curve.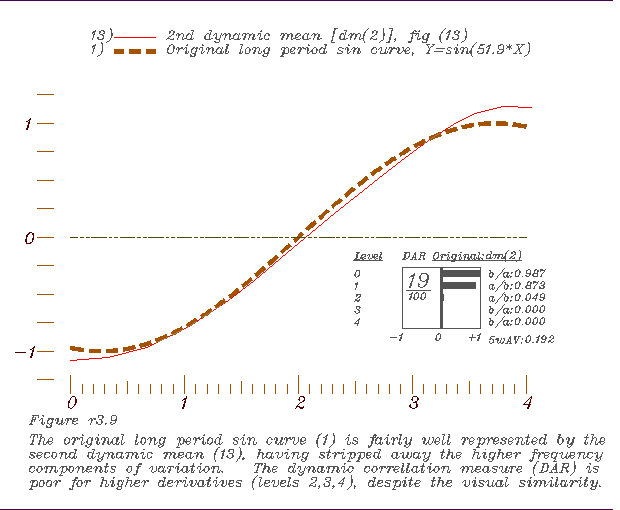 10. Comparing the 1st derivatives of the 2nd dynamic mean and the long
period sin curve,
10. Comparing the 1st derivatives of the 2nd dynamic mean and the long
period sin curve,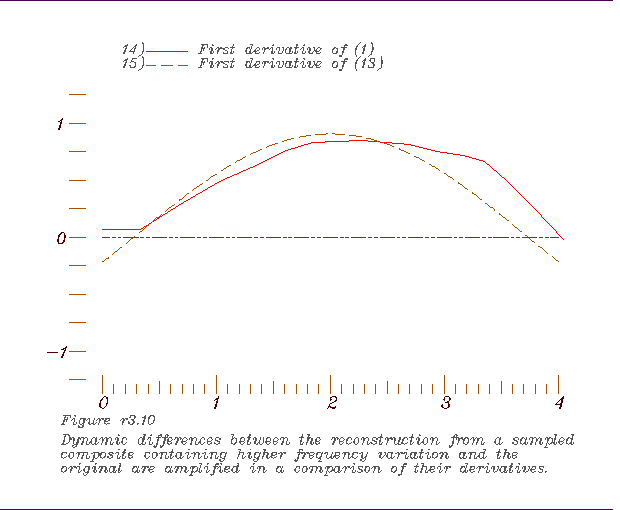 11. Comparing the residual of the 2nd dynamic mean and the 1st with the
medium period sin curve,
11. Comparing the residual of the 2nd dynamic mean and the 1st with the
medium period sin curve,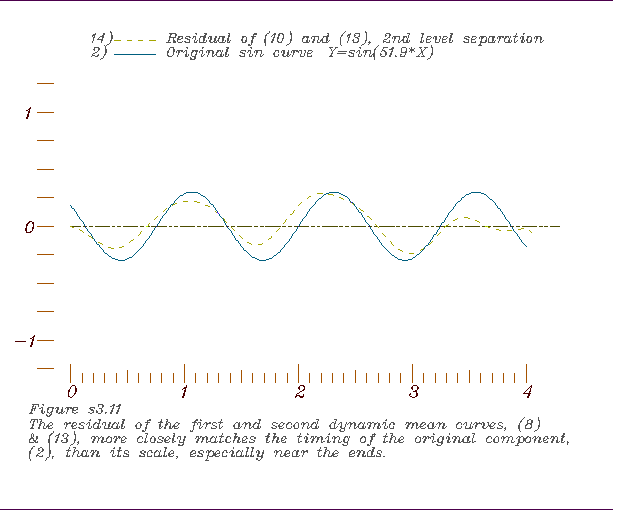 12. Comparing the residual of the 1st dynamic mean and the short period
sin curve
12. Comparing the residual of the 1st dynamic mean and the short period
sin curve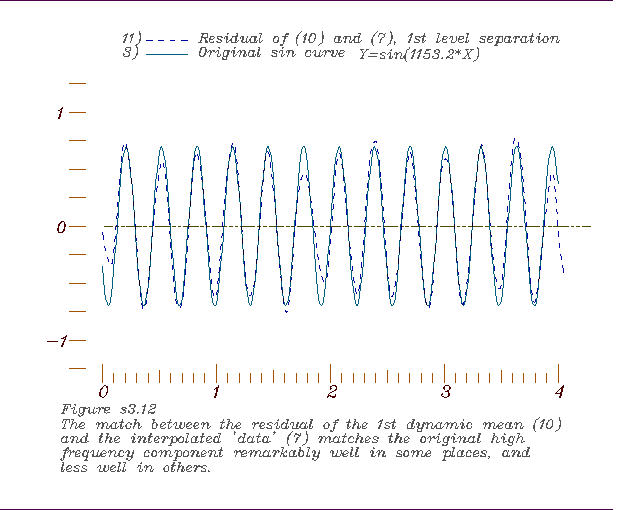
back to the DR main page