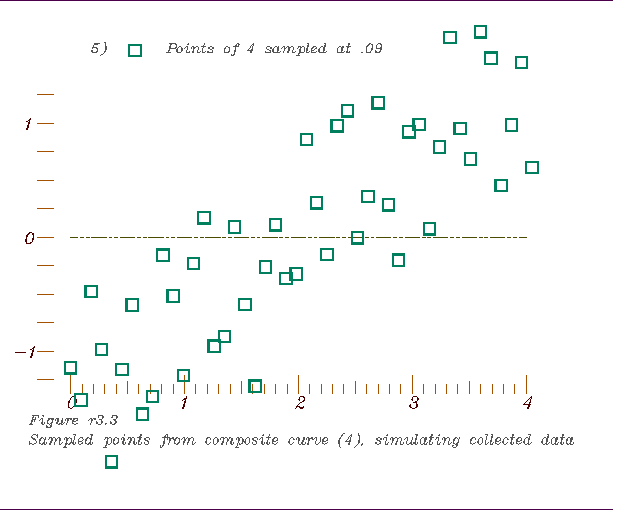Reconstructing a function from scattered
points
 A
demanding test of a time series shape recognition method is provided by
sin curves that are 'disguised' by superimposition and then sampled to
see if the components can then be reconstructed. Derivative reconstruction
(DR) performs admirably in this task as shown below. Time has not yet allowed
displaying the comparable performance of what seems to be the current state
of the art computer vision method, curvature scale space (CSC). CSC performs
admirably on many other tests. Investigation has shown it to be reasonably
effective in identifying the two longer period curves, but to lose the
higher frequency curve entirely. This is a function of the amount of information
present in the sampled data, and the smoothing 'kernel' that fundamentally
distinguishes the two methods.
A
demanding test of a time series shape recognition method is provided by
sin curves that are 'disguised' by superimposition and then sampled to
see if the components can then be reconstructed. Derivative reconstruction
(DR) performs admirably in this task as shown below. Time has not yet allowed
displaying the comparable performance of what seems to be the current state
of the art computer vision method, curvature scale space (CSC). CSC performs
admirably on many other tests. Investigation has shown it to be reasonably
effective in identifying the two longer period curves, but to lose the
higher frequency curve entirely. This is a function of the amount of information
present in the sampled data, and the smoothing 'kernel' that fundamentally
distinguishes the two methods.
The full size figures
display the steps of DR shape reconstruction in12 steps, from:
-
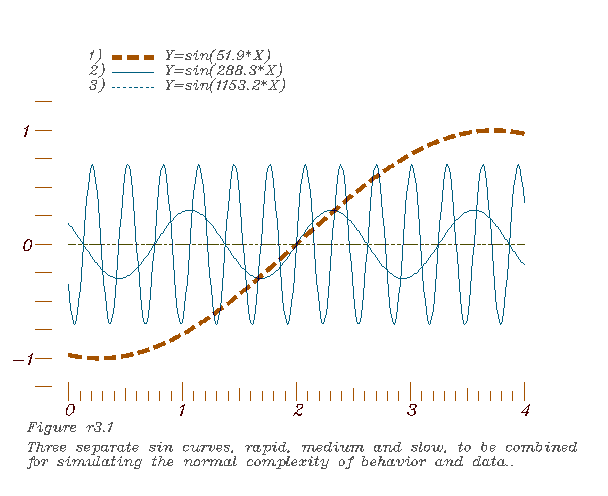
1. Selecting three regular mathematical sin curves,

-
2. Combining and sampling them to simulate the normal complexity of data
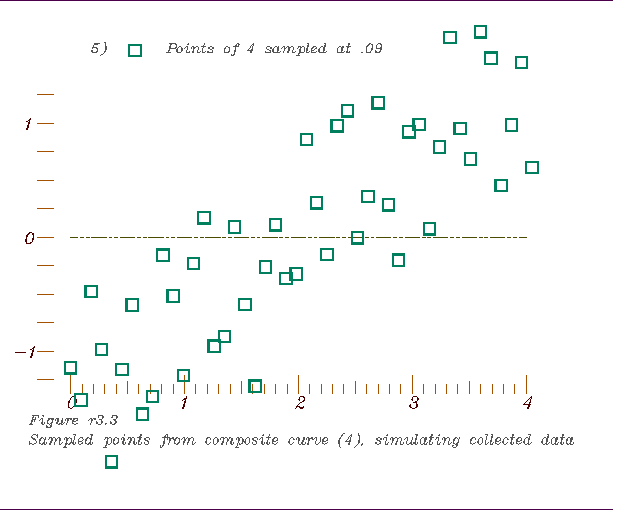
-
3. Comparing the continuities identified with the original.
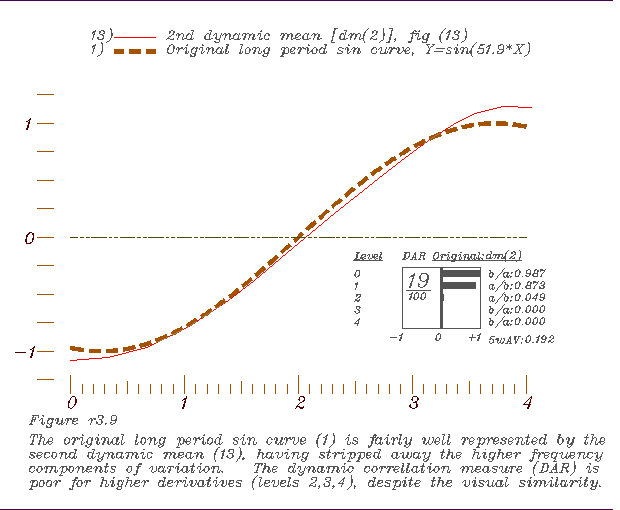
-
for more detail see the intermediate steps at full size by opening the
links in the table below
back to the top
 A
demanding test of a time series shape recognition method is provided by
sin curves that are 'disguised' by superimposition and then sampled to
see if the components can then be reconstructed. Derivative reconstruction
(DR) performs admirably in this task as shown below. Time has not yet allowed
displaying the comparable performance of what seems to be the current state
of the art computer vision method, curvature scale space (CSC). CSC performs
admirably on many other tests. Investigation has shown it to be reasonably
effective in identifying the two longer period curves, but to lose the
higher frequency curve entirely. This is a function of the amount of information
present in the sampled data, and the smoothing 'kernel' that fundamentally
distinguishes the two methods.
A
demanding test of a time series shape recognition method is provided by
sin curves that are 'disguised' by superimposition and then sampled to
see if the components can then be reconstructed. Derivative reconstruction
(DR) performs admirably in this task as shown below. Time has not yet allowed
displaying the comparable performance of what seems to be the current state
of the art computer vision method, curvature scale space (CSC). CSC performs
admirably on many other tests. Investigation has shown it to be reasonably
effective in identifying the two longer period curves, but to lose the
higher frequency curve entirely. This is a function of the amount of information
present in the sampled data, and the smoothing 'kernel' that fundamentally
distinguishes the two methods.