Key shapes
These shapes are commonly found in measures traced
over time. When significantly different states are found 'before'
and 'after', they reflect the development of the transition between them.

A.. A simple change of direction.
Periods reflecting different steady states (Black lines) when nature behaves
as if following different rules. A shape connecting them (Red
line) shows progression of change during the period that connects before
and after. The mathematical uniqueness of this shape is that
an infinite number of derivatives may exist and all have the same sign.
In a perfect continuum, for change to begin or end there must be finite
periods during which an infinite number of derivatives exist and have the
same sign, a 'law of continuity'.

B. A simple change of state.
This shape is also the rates of change (first derivative) of A
and the accumulated effect (the integral) of a simple whole event as in
C.
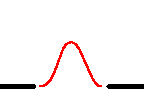
C. A simple whole event.
A passing 'bump' on a curve going from nothing to nothing, from before
beginning to after the end.
Actual data may contain influences from many different
things at once, displaying overlapping effects. The periods of constant
behavior may follow a 'constant' rule that is quite complex. There
might be too little data or the processes of organizational transition
might be expressed in different ways in the measure being used at different
times. It is also quite common that the 'states' of behavior
being monitored are in fact not highly organized and neither constant nor
transitional states can be found.
ed. 3/20/99


