Introductory notes for the Physics of Uncontrolled Systems
(general theoretical tools for observation and prediction)
Notes
on Causation
|
Explanatory causation |
Instrumental Causation |
|
- What is expected to happen - |
- What and how things happen - |
|
(in the mind) |
(in the world) |
|
defining
answers |
raising
better questions |
|
Aristotle's
Material, Efficient, Formal & Final cause |
Development & Learning Processes, Environments, Seed events, Accumulative path making, Emergence & Integration, Expanding & Contracting Exploratory Variation |
JL Henshaw id .at. synapse9.com 11/03, 07/08, 11/23/08 (needs an update) -
11/1/09 My work on constructing a physics of individual events that escapes the trap science constructed by describing complex physical processes as equations using statistics and categories represented by numbers. Some better questions can be framed in an answerable way using by finding a successful method of pointing to "things" beyond our information as the real subject of science. That's the focus of
· A general law of Emergence and Continuity in Change,
· the Energy physics of continuity discussion of principles
· the Chapters of whole events model of natural successions and
· The Physics of Happening and its statistical methods for exploring individually animated emerging systems.
2/10/11 In a nut shell, as a research physics method it leads to a procedure for linking equations that are defined only over finite periods, with a method of exploring the environmental processes connecting them. Those environmental processes involve multiple scales of organizational change that involve events and processes of accumulation beyond the domain of equations to define, needed to provide the physical continuity between definable states.
Energy using processes take a succession of stages
of alternating regularity and change
that can be explored and then represented using a energy accounting boundary as the basis for the conservation equations.
Ein = Eseed +Einv+ Eret+ Edev + Eop + Enet + Eloss+ Edisc (1)
Enet > 0 (2)
The above table of terms associated with causation is not discussed below. This page mainly discusses why there are two columns in the table, at all. Why is there anything to observe not implied directly by the laws of science? Why do we need to "go look" to see how things are happening by themselves? It's because the things in life that are most important and interesting to us involve local systems and local learning, that are generally not pre-determined. This method of research is about how to learn a great deal more about such individual local systems than ever before. Even when outcomes are quite predictable, natural mechanisms need to take place by exceedingly complex local development processes with a large potential for accumulative variation, and highly individualized outcomes. Things may unpredictably take off on directions of their own, so you wouldn't know unless you were watching for when and how that happens. If we're not watching and miss the signs of important complex systems change, it can have large consequences.
Uncovering what makes math work - the continuity of physical systems
The reason measurement is useful and why math works to explain things in nature comes from the emergent physical property of natural systems, an organizational property of having changes that are accumulative.. and are said to be "conserved". That energy is "conserved", for example, is both a statement about the processes that use it, that they are strictly accumulative, as well as about the outcome. Only a little closer look implies ¸¸¸.·´ ¯ `·.¸¸¸ the continuity of comings and goings and the conservation of accumulative change in its processes.
When nature works like an adding machine, we get to use math to describe it. We don't think that origin of math often, but the even the tendency of "things in motion to remain in motion" and the conservation of space and time are emergent properties of the universe, and the reasons why our equations for geometry and motion work. If changes are conserved adding one amount makes the thing added to that much larger. That's what makes addition and subtraction useful. If change is not accumulative, but discontinuous, math for it wouldn't work. Even when accumulations of change are not conserved, and math seems useless, there's still another hidden feature of change that can make it useful again. That's identifying the locally conserved continuity of change and it's temporary conservation of rates of developmental change. What it opens up is a world of good questions about the instrumental processes that one observes the results of. It's the continuity of change processes that is conserved even when the changes themselves are not. It's watching the continuities shift that becomes a key to watching how they work.
Continuity + Change = "little bangs" followed by "big booms" ... a whole process
The math to explain why continuity is 'eventful' comes from exploring a basic contradiction in the laws of physics. The conservation principles of energy, momentum and reaction forces are the three principles that form the foundation of physics. The trouble is that if anything followed them perfectly, nothing in nature could begin or end. It's just such contradictions in our expectations for things that have forced new discoveries many times in the past. It turns out that the statements of these three laws are interrelated, and actually state just one law, a general principle of continuity in change. It's that principle of continuity that is apparently violated by the observation that things in nature do definitely begin and end.
What is actually implied by the conservation laws and the common principle of continuity they imply, is that no accelerations of energy transfer can be infinite, so change can have no discontinuous jumps. How nature manages to put together those flows is what you look for in all the kinds of events that begin and end.
An intriguing corollary, a general principle of change, describes a mathematical trick for satisfying both continuity and change, and is strongly supported by observation as being like the way nature does it too. You might say that discontinuity in nature is so very difficult, that to do it takes processes of explosion, things that develop with a "boom" having started with "little bangs". The mathematical physics theorem describing the particulars to how that has to happen is about how energy flows need to begin or end. Nature requires scales of complexity to do it, so events can erupt from scale to scale, constructing natural systems of energy transfer within the constraints of the Law of Continuity and The energy physics of Continuity in Change. It points to the fine details of natural processes that are easy to miss, unless you're watching and know what to look for. When we're not looking for them the 'booms' of growth processes just look like some unexplained machine, and only when you know what to look for is it apparent that they are express systems that are actively evolving as they operate, not following a 'script'. One hint is that growth processes generally start with some 'seed' event, a "little bang" of emergence, germination, conception, fertilization or someone's great idea, etc. That these events are so "quick" and "smooth" at the same time has meant it was hard to catch them at what they were doing. Science also hadn't found a way to use math to describe them and no one thought of using math backwards, as a diagnostic tool instead, to help explore them. When you study things that exhibit growth you do definitely find the emergent systems producing them too, and vis-a-vis, but we just had not been looking. It explains a great deal about why both our common awareness and interest in systems of change and the study of the uncontrolled systems on which we so heavily rely have been so lacking.
Energy can neither be created or destroyed, and changing it into other forms or moving it from place to place requires that processes to do that start and stop. That takes developing a process to do it. Because we can watch energy flows, we can then often locate the 'little bangs' that set off the 'big booms' of process development. It's the developmental continuity that is conserved when every thing else may not be. The signal to watch for is the divergence, the progressions of change of any sign where all the derivatives of change are of the same sign. That's it. Such progressions point to where and how the organization of the physical processes involved are accumulating irreversible organizational changes, and signal how those changes are interacting with their environments. It amounts to a principle that at the beginning of any process of lasting change there's a period of "inflation", a boom of development, just like (and for about the same reason as) there is thought to have been a period of inflation to initiate the "Big Bang" of the universe. You can use that clue in the data as a pointer to finding some of the smaller developing new worlds that they signify, to study them and what they're likely to run into..
07/08 (i.e. older) The real physics of change for natural systems is about how systems that use energy accumulate and dissipate their organization. Organization does not have deterministic "causes and effects". It has processes of development and decay. Divergence is a sign organizational development or decay, and of where to watch to discover how it works. Organization processes tend to be an individual and localized, but they also often become more complex or have many different ones overlapping in a shared environment. Organization is never transferred, though. It only develops. Even though the parts of different ones may be mixed, separate organizational processes may be quite distinct, like different communities sharing the same neighborhood. Only exceedingly simple and predictable organization can be represented by our information. Open system organization needs to be represented by itself, and only referred to by our information.
Learning to observe the processes that perform the magic becomes a powerful new research tool, much as learning about the conservation of energy was for classical physics. It offers an unusual new window into nature to use the derivative continuities (shapes) that come and go in the curves of physical measures to locate the little bangs that mark the emergence of organization. Coupled with direct exploratory observation of the environment, studying how individual development processes create their conserved organization exposes them as as path-finding rather than rule-following mechanisms.
Physical systems are quite unlike theoretical models, so for theoretical scientists it would be a little like watching the physical world as if it were an "in-physico model". I put it in that odd way because usually natural systems are thought of by theorists as being sets of equations and the data curves displaying behaviors of physical processes are thought of as implied equations as well. Those equations, however valid statistically, hardly hint at the complex organization of the physical behaviors they simplistically emulate. For example, the height of a person doesn't tell you much, but when that's all the information you have, people habitually make the reductionist step and represent the person as a number. Remembering that reality is more than our information is as easy as using the information to refer back to where it came from. It's the same for the relation between a model and the system it represents, thus my term "in-physico model". The classic dynamic processes of conserved change are growth and decay. The systems that accumulate conserved change appear to follow the general principle of change, continuity and divergence, that it takes a conserved process to change a conserved process, and you can locate them with the 'little bangs' at the beginning and end of events.
Another implication of the conservation of change is that if a process shows evidence of being conserved, but you see discontinuities in it, the continuity is probably located somewhere you're not looking. It's a wonderfully useful research guiding rule, not an excuse. It's the rule that says why you will often not see how nature connects the dots. For universally conserved properties like energy, the law of continuity assures that "the dots are connected" by some process, however, and helps one find them.
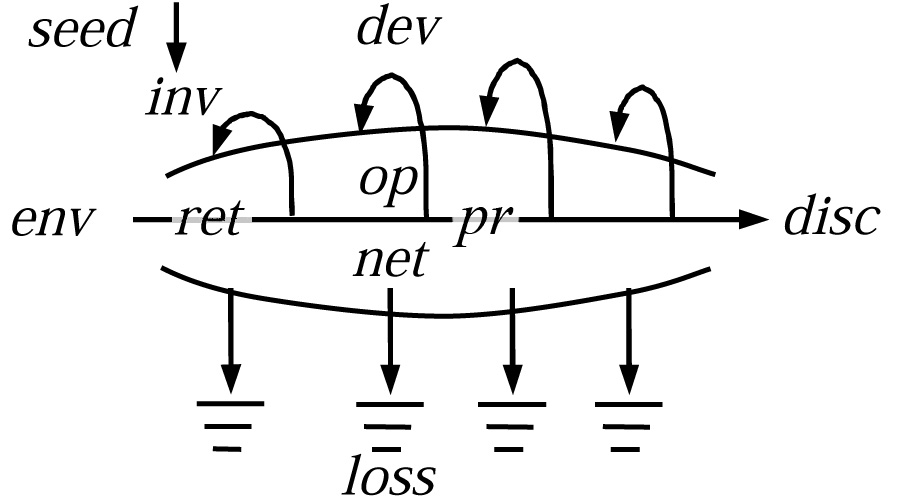
Discovering how individual mechanisms of conserved change develop and decay can be aided by using a standard diagram for development and decay, displaying dynamical markers for the series of transformations required by continuity. Period from points 1 to 2 is the 'little bang'. One may see a precursor event at point 1, like a spark to start the fire by initiating the inflationary period of its development. Initial sparks that trigger inflationary processes are usually so small and so quick they're only hypothesized. Continuity of the flow of energy requires one to presume that they or something like them is there though. Our information is just incomplete, because the start of things that begin with a burst are inherently untraceable. What the diagram provides is an efficient question generating model for what is observable. It uses the data available to direct attention back to the physical environment and the process developments, in context, to help locate where and how the natural developmental instabilities will take place. It's not good enough to just say "things come and go so we can't predict". Reading the map lets you ask when a 'little bang' is going to peter out or collide with other things producing cascades of environmental conflicts.. for example. It's a set of leading questions that enables you to go find out what's really happening.
0 ![]() 1
1 ![]() 2
2![]() 3
3 ![]() 4
4 ![]() 5
5![]() 6
6![]()
... A Couple Problems Of Temporal
Physics:
11/23/03 07/08 (i.e. older) How nature works can be approached several
ways. Physics conventionally studies the universal properties of
things and how those properties are mathematically related. The
approach here is about how natural processes develop new temporarily stable
relationships, and could be called temporal physics. The emergent
processes and relationships of systems are not transported from somewhere else,
but develop in what amount to little universes of their own. That
makes this the study the unique local properties of things and how they
evolve.
For example, you might ask, why natural
systems can seem unusually resilient some times and at others to seem to
abruptly fall apart? The trick I use is that in the process of
doing that, there are progressions of change that are conserved.
People are inclined to grasp at grand rules, like using the tautological
argument of survival that only what survives exists to be observed, so
everything can be explained as a balance between a universal tendency to
collapse and a rare random occurrence of order. I think it's better
to watch and see rather than cast about 'incontrovertible'
hypothesis. For example, it's particularly curious how useful the
'chaos' of open environments are, allowing the resources for one thing to be
waste products of others (interdependence) being exchanged like messages in a
bottle through common exchange mediums like blood streams, fresh water ponds,
the air, oceans, open land etc. The observation that systems make
very good use of the chaotic mess around them is like a starting point for real
inquiry.
Usually the 'ah ha' moment comes toward
the end of your stamina, when in desperation with stalled progress you stumble
on some little thing and discover you've been approaching the question all
wrong...and lets you proceed to complete the task. Once you collect
all the pieces of the problem you need to transform them before you can
distribute the results. Collect, transform & distribute a whole
system learning process, what I call a whole event, with the same stages of
beginning and ending conserved change for your learning as for any other
system's, and you can identify some of the particular learning path inventions
when you trace its energy flows or other conserved properties.